The Fibonacci sequence is a mysterious mathematical series that has been linked to several natural phenomena and has a wide number of applications in stocks, trades, and science. In this article, you will learn about the Fibonacci sequence and how to calculate it with the help of Excel. You will also learn how the Fibonacci sequence is related to the Golden ratio and how to calculate it. We have also attached a practice worksheet. Click in the below download box to get the practice file.
1. What Is the Fibonacci Sequence?
The Fibonacci sequence is a series of numbers starting from 0 and 1 that advances so that a number is equal to the summation of the previous two numbers.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…………
It is named after the Italian mathematician Leonardo Fibonacci who developed the sequence in the 13th century. On the other hand, some historians also claimed that the sequence is found in the Hindu-Arabic numerical system from ancient Sanskrit text. But in 1202, Leonardo Fibonacci published a mathematical book Liber Abaci. This textbook introduced the benefits of this Hindu-Arabic numerical system to calculate and predict the profits and losses in trades, barter, money changing, conversion of weights, and measurements.
2. How to Find the Fibonacci Sequence in Excel
It's easy to find the Fibonacci sequence in Excel. The Fibonacci sequence is calculated by adding the two previous numbers.
For example,
n = 0, 1, 2, 3, 4, 5……..
So, the Fibonacci numbers will be,
X0 = 0
X1 = 1
X2 = X1 + X0 = 0 + 1 = 1
X3 = X2 + X1 = 1 + 1 = 2
X4 = X3 + X2 = 2 + 1 = 3
X5 = X4 + X3 = 3 + 2 = 5
So, the general formula to calculate the Fibonacci number is,
Xn = Xn-1 + Xn-2
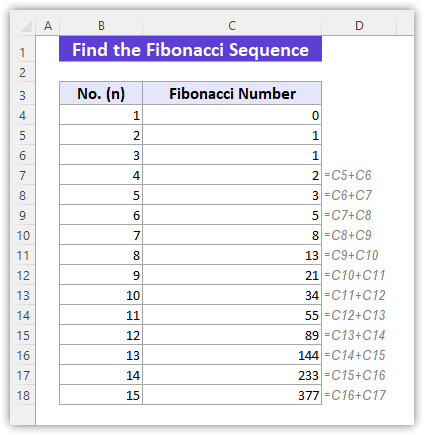
- To find the sequence in Excel, we will sum two numbers 0 and 1 in the C4 and C5 cells.
- Enter the formula in cell C6 to sum the numbers:
=C4+C5

- In cell C6, it will return 1.
- Now, AutoFill the next cells to find the next Fibonacci numbers.
3. How to Use the Fibonacci Sequence to Calculate the Golden Ratio
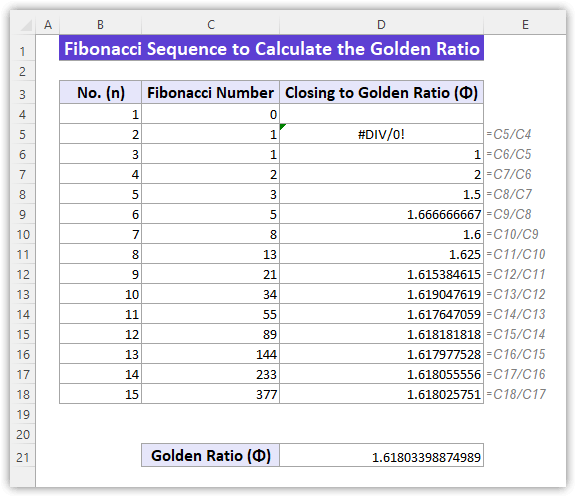
Here is a surprising fact about the Fibonacci number you can get the value of the Golden ratio (𝚽 = 1.61803398874989) by dividing the two successive Fibonacci numbers (337/233 = 1.61805555555556). The bigger we take the two Fibonacci numbers the closer we will reach to the Golden ratio 𝚽.
- In cell D6, enter the following formula to divide the two Fibonacci numbers:
=C5/C4

- Now, AutoFill the next cells to find the ratio value of the two Fibonacci numbers.
- See the image below that the ratios are getting closer to the value of the Golden ratio 𝚽.
4. How to Use the Golden Ratio to Find the Fibonacci Sequence
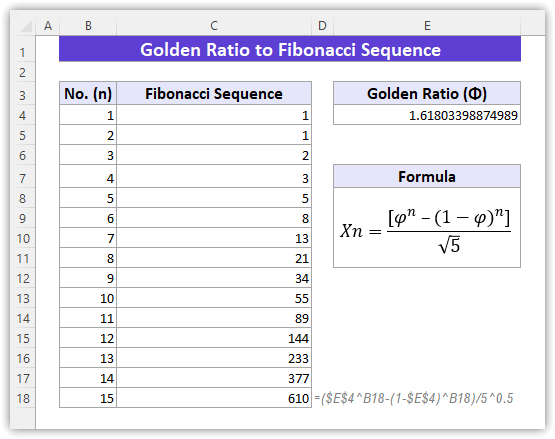
As you can calculate the Golden ratio 𝚽 from two Fibonacci numbers, you can also find the Fibonacci sequence from the Golden ratio 𝚽 vice versa.
Here is the formula to calculate the Fibonacci numbers,
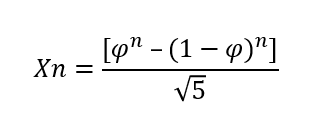
n = Fibonacci Serial number
Xn = Fibonacci number
- Enter the formula in Excel to calculate the Fibonacci number:
=($E$4^B4-(1-$E$4)^B4)/5^0.5

- Now, AutoFill the next cells to find the next Fibonacci numbers.
5. What Are the Fibonacci Sequences in Nature?
There are so many miraculous phenomena around the universe linked with the Fibonacci sequence. Have a look at some of the greats from them:
- The petal numbers in flowers always follow the Fibonacci numbers (21, 34, 55, etc.)
- Tree branches split in the Fibonacci sequence from the ground.
- Snail shells form the shape of a Fibonacci spiral.
- The spiral galaxy forms a similar shape to the Fibonacci spiral.
- Hurricanes spirals are another example of the Fibonacci spiral.
- Look at the fingers and the bones: the ratio of the immediate larger portion to the smaller portion is nothing but the golden ratio.
- Human faces also resemble the golden ratio. If you subdivide each portion (mouth, nose, eyes, ears, chin, etc.), you can find the existence of the Golden ratio each time. So, it is also known as God’s ratio or the ratio of the creation.
- More surprisingly, the Fibonacci sequence exists in DNA. The DNA molecule's dimensions for a complete cycle of its double helix spiral are approximately 34 angstroms in length and 21 angstroms in width. Notably, these values, 34 and 21, are part of the Fibonacci sequence, and their ratio closely approaches the Golden ratio.
6. How Can the Fibonacci Sequence be Related to Trading Behavior
The Fibonacci sequence is quietly related to real-life trading behavior. Traders or investors can predict the retracement levels of the market price of an asset. The most commonly used Fibonacci ratios in trade are 0.236, 0.382, 0.5, 0.618.
For example, the price of an asset is $100 and suddenly the price rises to $140. So, we want to find the retracement levels to predict where the price may retrace or extend.
Price difference = $140 - $100 = $40
At a 23.6% retracement level price would be: $100 + ($40*0.236) = $109.44
At a 38.2% retracement level price would be $100 + ($40*0.382) = $115.28
At a 50% retracement level price would be $100 + ($40*0.5) = $120
At a 61.8% retracement level price would be $100 + ($40*0.618) = $124.72
Conclusion
From the whole article, you have learned about the Fibonacci sequence and how to calculate it with the formula. We hope this article will help you to use the Fibonacci sequence in creating new sequences and forecast trades prices. You can share your thoughts with us in the comment section or ask for any queries about this article. Good Luck!
Tags: Range